Просто совпало высвобождение. ДС от закрытого ИИС и снижение курса валюты, решил "отщипнуть" для эксперимента и диверсификации, это всего 10% от портфеля (не великого). К слову, на те же 10% суммарно я набрал и длинных рублёвых ОФЗ. Момент входа по ОФЗ не угадал, вёз минус, за последнюю неделю решил его ликвидировать, "преобразовав" в отрицательную НОБ и отложив налоги "на потом"..Смотрю на Вас , как у Вас менялось мнение про длинные облигации , например ОФЗ-Н , получили опыт, а потом начали более осторожно действовать , про облигации в юанях, только недавно мы с Вами беседовали.
Вы используете устаревший браузер. Этот и другие сайты могут отображаться в нём некорректно.
Вам необходимо обновить браузер или попробовать использовать другой.
Вам необходимо обновить браузер или попробовать использовать другой.
-
ОПРОС ПО СТАВКАМ
Ставки по НС и коротким вкладам (до шести месяцев) через полгода будут ниже или выше чем сейчас?
Принять участие в опросе можно здесь.
Облигации. Вопросы новичка (читает 1)
- Автор темы kulakov
- Дата начала
kulakov
Мастер
- Сообщения
- 814
- Спасибо
- 437
- Город
- Москва
- Стаж c
- 31.08.06
- Опыт
- 3155/288
К сведению (программистов?), оказалось, что краткие названия облигаций неуникальны глобально, т.е. сейчас появилась БалтЛизБП1, к-я раньше уже была. Подробнее расписал на СЛ.
kulakov
Мастер
- Сообщения
- 814
- Спасибо
- 437
- Город
- Москва
- Стаж c
- 31.08.06
- Опыт
- 3155/288
Случайно обнаружил, что у многих облигаций с пут-офертами в дату изменения купона также есть как бы скрытые колл-оферты. Они конечно не скрытые сами по себе, т.к. в программе облигаций про них написано, просто про них обычно сложно найти информацию. Подробно расписал на СЛ.
Я не понимаю, почему Мосбиржа указывает
https://www.moex.com/ru/issue.aspx?board=TQCB&code=RU000A107UU5
для облигации RU000A107UU5 доходность при текущей цене (чуть более 100%) более 17.3% при купоне 16.5 % ? Как такое может быть ? При цене в 100% доходность равна купону, больше цена - доходность ниже.
https://www.moex.com/ru/issue.aspx?board=TQCB&code=RU000A107UU5
для облигации RU000A107UU5 доходность при текущей цене (чуть более 100%) более 17.3% при купоне 16.5 % ? Как такое может быть ? При цене в 100% доходность равна купону, больше цена - доходность ниже.
anatolius
Мастер
- Сообщения
- 989
- Спасибо
- 490
- Стаж c
- 12.08.12
может из-за близости даты выплаты купона?Я не понимаю, почему Мосбиржа указывает
https://www.moex.com/ru/issue.aspx?board=TQCB&code=RU000A107UU5
для облигации RU000A107UU5 доходность при текущей цене (чуть более 100%) более 17.3% при купоне 16.5 % ? Как такое может быть ? При цене в 100% доходность равна купону, больше цена - доходность ниже.
В каком смысле близкой ? Выплата там ежемесячная, прошлая была (номинально) два дня назад. В БКС и ВТБ купон еще не пришел.может из-за близости даты выплаты купона?
Verges
Мастер
- Сообщения
- 734
- Спасибо
- 1,623
- Город
- Санкт-Петербург
- Стаж c
- 01.04.15
- Опыт
- 2134/746
При цене 100% эффективная доходность YTM (а именно ее показывает биржа) больше ставки купона.Я не понимаю, почему Мосбиржа указывает
https://www.moex.com/ru/issue.aspx?board=TQCB&code=RU000A107UU5
для облигации RU000A107UU5 доходность при текущей цене (чуть более 100%) более 17.3% при купоне 16.5 % ? Как такое может быть ? При цене в 100% доходность равна купону, больше цена - доходность ниже.
Для данной бумаги купон = 16,25%
Прикидка для YTM = (1+16,25%/12)^12 - 1 = 17,51% (для цены 100%). Именно столько и показывает.
Эффективная = YTM ? YTM при цене 100% очевидно = ставке купона (без учета малых поправок за счет НКД). Я полагал, что Мосбиржа YTM показывает.При цене 100% эффективная доходность YTM (а именно ее показывает биржа) больше ставки купона.
Для данной бумаги купон = 16,25%
Прикидка для YTM = (1+16,25%/12)^12 - 1 = 17,51% (для цены 100%). Именно столько и показывает.
Verges
Мастер
- Сообщения
- 734
- Спасибо
- 1,623
- Город
- Санкт-Петербург
- Стаж c
- 01.04.15
- Опыт
- 2134/746
Это не очевидно, а просто неверно.Эффективная = YTM ? YTM при цене 100% очевидно = ставке купона
YTM - это и есть эфф. доходность, которую и показывает биржа.
При цене 100% ставке купона будет равна простая доходность.
А эффективная больше простой (при выплатах чаще, чем раз в год).
Аналог - вклад под номинальную ставку 16,25% с ежемесячной капитализацией. Эффективная доходность будет как написал выше.
Если я и ошибаюсь, то вместе с Википедией https://ru.wikipedia.org/wiki/Доходность_к_погашениюЭто не очевидно, а просто неверно.
"2. Если купонная доходность равна YTM, то облигация должна продаваться точно по номиналу."
"If a bond's coupon rate is equal to its YTM, then the bond is selling at par." https://en.wikipedia.org/wiki/Yield_to_maturity
kulakov
Мастер
- Сообщения
- 814
- Спасибо
- 437
- Город
- Москва
- Стаж c
- 31.08.06
- Опыт
- 3155/288
Ну где ж вы были раньше, это всё уже обсуждалось.Эффективная = YTM ?
Мало того, что считается эфф. доходность для бумаг, у к-х до погашения ещё много времени, проблема в том, что если до погашения остался месяц, то там будет такой же эффект, даже если купон был раз в год.
Как это ни странно, Вика тут не ошибается. Для того, чтобы это понять, надо учесть 2 нюанса.Если я и ошибаюсь, то вместе с Википедией
1. Там предполагается, что купоны платятся раз в полгода (ну у большинства это так)
2. Там предполагается, что Ytm считается не для года, а для полугода (стандарт в долларовой зоне, в отличие от года в рублёвой зоне).
На нашей бирже по долларовым бумагам это тоже так, кстати.The YTM is often given in terms of annual percentage rate (APR), but more often market convention is followed. In a number of major markets, the convention is to quote annualized yields with semi-annual compounding
И т.к. эти сроки совпадают, простая доходность = эфф.дох. при цене 100.
Мало ли дел может быть.Ну где ж вы были раньше, это всё уже обсуждалось.
Как это ни странно, Вика тут не ошибается. Для того, чтобы это понять, надо учесть 2 нюанса.
1. Там предполагается, что купоны платятся раз в полгода (ну у большинства это так)
2. Там предполагается, что Ytm считается не для года, а для полугода (стандарт в долларовой зоне, в отличие от года в рублёвой зоне).
На нашей бирже по долларовым бумагам это тоже так, кстати.
И т.к. эти сроки совпадают, простая доходность = эфф.дох. при цене 100.
Ничего такого там явно не предполагается. Все что говорится про более частые выплаты, это: "Аналогичным образом можно записать уравнение для любого количества выплат в течение года. Для этого достаточно вместе множителя (делителя) 2 взять множитель (делитель), равный количеству выплат." А потом уже процитированное (безотносительно к продолжительности купонного периода): "Если купонная доходность равна YTM, то облигация должна продаваться точно по номиналу". А между строк я читать не умею.
Verges
Мастер
- Сообщения
- 734
- Спасибо
- 1,623
- Город
- Санкт-Петербург
- Стаж c
- 01.04.15
- Опыт
- 2134/746
Не надо читать между строк. Нужно правильно понять определение доходности к погашению, данное в википедии.Ничего такого там явно не предполагается. Все что говорится про более частые выплаты, это: "Аналогичным образом можно записать уравнение для любого количества выплат в течение года. Для этого достаточно вместе множителя (делителя) 2 взять множитель (делитель), равный количеству выплат." А потом уже процитированное (безотносительно к продолжительности купонного периода): "Если купонная доходность равна YTM, то облигация должна продаваться точно по номиналу". А между строк я читать не умею.
Из формул видно, что при расчете доходности к погашению это значение приводится именно к длине купонного периода.
Иными словами, для годового купона - к году, полугодового - к полугоду, аналогично для ежемесячного купона - к месяцу.
При таком подходе точно так и будет: при цене 100% такая доходность к погашению в точности равна купону.
Для примера, пусть есть вклад под 16% годовых на год. (Либо облигация с аналогичными параметрами выплат).
Три варианта выплат:
- раз в год;
- дважды в год;
- ежемесячно.
По правилам википедии для этих вариантов доходность к погашению будет: 16%; 8%; 1,333% соответственно.
Понятно, что для целей сравнения разных инвестиций это неприемлемо.
Поэтому всегда считают доходность к погашению, приводимую к одному и тому же сроку (к году, в большинстве случаев).
Тогда для этих вариантов получится:
16%
16,64%
17,23%
Именно такой будет доход для приведенных примеров. И можно сравнивать.
Мосбиржа считает, приводя доходность к погашению всегда к году:
https://fs.moex.com/files/6908/
(В формуле 11 есть число 365).
Кстати, формулы в википедии никак не могут быть применены, например, для переменного купона (по величине и/или по длительности), для облигаций с амортизацией и других не самых простых случаев.
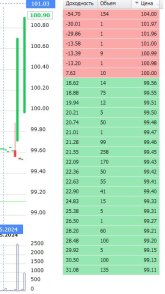
Всё же очень интересует меня вопрос - зачем люди ЭТО делают?.. С какой целью? Один раз можно чисто технически ошибиться, так ведь не успокоились на 100.7, добавили до 100.9!
Я, конечно, такого не ожидал никак, слил всё чуть меньше 100%, т.к. это лотерея. Возможно, знай я цель подобных "запусков", сдал бы ещё более удачно?..
З.Ы.: продавцы, видя такое целенаправленное действо, совсем уже попёрли в дурь - покупают по любым ценам!...
Я, конечно, такого не ожидал никак, слил всё чуть меньше 100%, т.к. это лотерея. Возможно, знай я цель подобных "запусков", сдал бы ещё более удачно?..

З.Ы.: продавцы, видя такое целенаправленное действо, совсем уже попёрли в дурь - покупают по любым ценам!...
Вложения
Последнее редактирование:
Struzhkin
Мастер
- Сообщения
- 5,225
- Спасибо
- 4,357
- Город
- Москва
- Стаж c
- 16.04.17
- Опыт
- 15944/796
Как тогда вот это объяснить?берут, с чего вы взяли что не берут?
https://hranidengi.com/threads/mkb-investicii.236/#post-65401
Там и скрин есть..Сегодня обнаружил что последний купон в МКБ-онлайн (02.05 Беларусь07) пришёл на банковский счёт без удержания НДФЛ!!
Или просто очередные выкрутасы "погромистов" МКБ?
@Struzhkin, почему-то сначало про ИИС подумал. Да на обычном брокерском такое может быть. Еще с прошлого года вроде как с купонов некоторые брокеры берут налог в конце года.
Struzhkin
Мастер
- Сообщения
- 5,225
- Спасибо
- 4,357
- Город
- Москва
- Стаж c
- 16.04.17
- Опыт
- 15944/796
Ну то что при выплате на брокерский так делают - это понятно. На брокерском счёте можно примерную сумму ДС под конец года оставить.Еще с прошлого года вроде как с купонов некоторые брокеры берут налог в конце года.
Но откуда брокер будет брать налог, если он всё перевёл в банк?..
Хорошо, если просто извещение на эти копейки в ФНС передаст.
видимо как и раньше, если все переводишь то налог удержат при выводе.Но откуда брокер будет брать налог, если он всё перевёл в банк?..
Похожие темы
- Ответы
- 208
- Просмотры
- 27K
- Ответы
- 8
- Просмотры
- 935
- Ответы
- 201
- Просмотры
- 21K
- Ответы
- 2
- Просмотры
- 1K
- Ответы
- 6
- Просмотры
- 1K
Просматривают тему:
Всего: 2 (пользователей: 0, гостей: 2)
Статистика форума
Новые темы
Новые записи блогов
-
Индекс настроения вкладчика (март 2026)Опрос будет закрыт через 3 дня Предыдущие опросы и их результаты
- UnembossedName
- Обновлено:
- 1 мин.
-
Почему выгодно использовать для дистанционного банкинга операционную систему Haiku?Почему выгодно использовать для дистанционного банкинга операционную...
- камо
- Обновлено:
- 1 мин.
-
Хардфорки Биткоина: что это, зачем их создают и какие есть варианты получения дохода?Хардфорк — значительное обновление протокола блокчейна, по итогу...
- Roman Moris
- Обновлено:
- 3 мин.
-
Как работать на УСН с 2026 годаКлючевые реформы УСН в 2026 году: что важно знать бизнесу С 2026 года...
- TARKI
- Обновлено:
- 2 мин.
-
Индекс настроения вкладчика (февраль 2026)Предыдущие опросы и их результаты Количество значимых голосов: 102...
- UnembossedName
- Обновлено:
- 1 мин.
Новые комментарии
-
Почему выгодно использовать для дистанционного банкинга операционную систему Haiku?В случае ошибок в работе приложения ОС Haiku предоставляет информацию на выбор пользователя /без использования кодов ошибок/ - обычно я сохраняю...
-
Почему выгодно использовать для дистанционного банкинга операционную систему Haiku?Нет таких кодов, поэтому нет расшифровки. Ибо ненужно

-
Почему выгодно использовать для дистанционного банкинга операционную систему Haiku?Есть специальное приложение для обновления всех пакетов ОС/в том числе и драйверов/ и пакетов приложений до их актуальной версии. И никаких...
-
Как работать на УСН с 2026 годаУСН 2026 стала проще формально, но на практике бюрократия растет, особенно с НДС и документированием расходов
-
Почему выгодно использовать для дистанционного банкинга операционную систему Haiku?Не надо за менять решать, что я считаю. Тем более, что я этого не говорил. Но есть ли у Haiku автообновления драйверов, в чаcтности? Есть ли...